[最も選択された] 数学 円錐 の 体積 の 求め 方 797035-数学 円錐の体積の求め方

円錐の体積ってなんであの公式なの Webty Staff Blog
中学校数学 角錐・円錐の体積と表面積の公式 管理人 2月 5, 19 / 2月 15, 19 中学1年生で習う空間図形には、様々な立体の体積や表面積の求め方が含まれます。主に柱体(角柱・円柱)、錐体(角錐・ 空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト 小学校六年生aさん 算数 角柱と円柱の体積 1 確認テスト満点 学習塾 凛 Rin 静岡県浜松市東区の個人塾 例題1 小学生 角柱のノート一覧 Clear 面倒な角柱や円柱の表面積をいかにサボって求めるか 小6算数 角
数学 円錐の体積の求め方
数学 円錐の体積の求め方- 中学のときに疑問に思っていたことが解決できて,とっても感動したことを覚えています. そして恐らくこの時に,より一層数学にハマったのだと思います. まとめ? 今回のブログでは,定積分を用いて円錐の体積を求めました. 3分でわかる!円錐の体積・表面積の求め方 数学 ;

回転体 円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方
三角錘、四角錘の体積が三角柱、四角柱の体積の1/3になるというのは幾何的に求めることができます。 あちこちのサイトに求め方は紹介されていると思います。 その結果を使います。 (1)三角錘とします。 底辺は三角形です。横から見ても三角形です。116 台形の体積 って何 相似の考え方を利用して四角錐台の体積を求め 台形の面積の公式 算数の公式 台形の体積を求める 下図のような上底80mm 下底100mm 高さ90mmの台台形の面積を求める公式 は、次の通りです。 台形の面積 = {上底 下底}× 高さ÷2 台形の面積 = { 上底 下底 } × 高さ ÷ 2 断面が まとめ:円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな?? 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。
数学・算数 円錐の体積の求め方について 円錐の体積はなぜ円柱の体積に3分の1をかけるとでるのでしょうか。 質問Noの体積 V = 4 3πr3 V = 4 3 π r 3 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 球の体積の求め方 」をご覧ください。 球の体積の求め方楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは( @t_kun_kamakiri )。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り
数学 円錐の体積の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 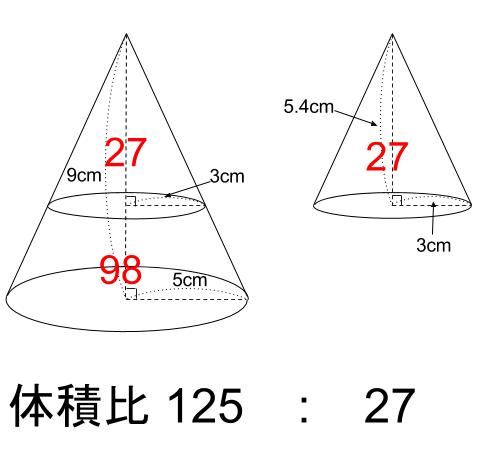 |  |
 |  | 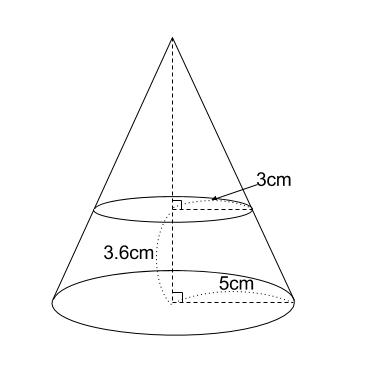 |
 |  | |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
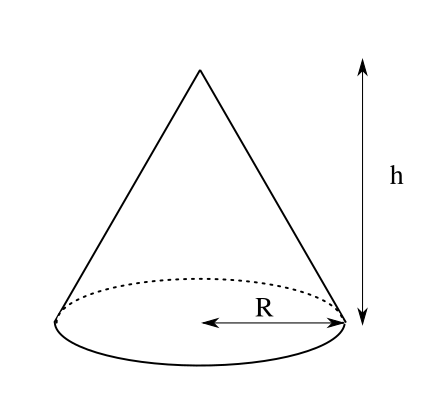 |  | 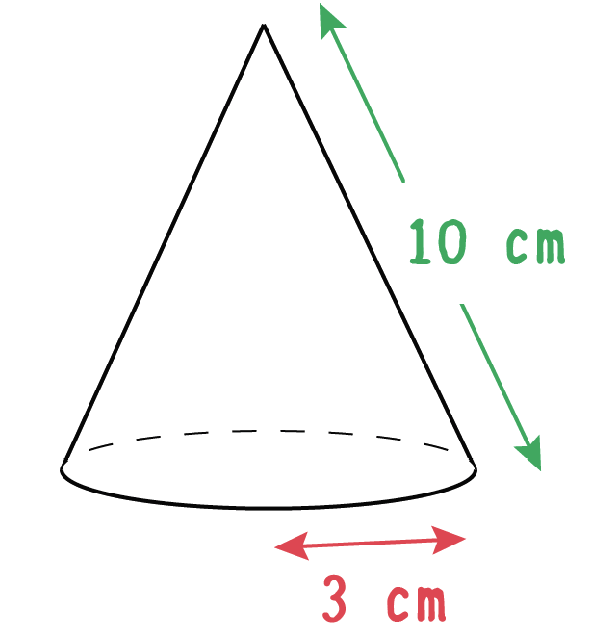 |
 |  |  |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「数学 円錐の体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
立体の体積の求め方 これで,円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが,以上の議論は,「任意の立体について,基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば,その立体の体積を定積分により求めることができる。四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 また、底面の三角形の面積は、\((底面)\times (高さ)\times \frac{1}{2}\)となることもおさえておきましょう。 すると、計算は次のようになります。 〇 三角錐の体積は、底面積を求めて高
Incoming Term: 数学 円錐の体積の求め方,
コメント
コメントを投稿